Pulsarwaarneming met een eigen RTL-dongle

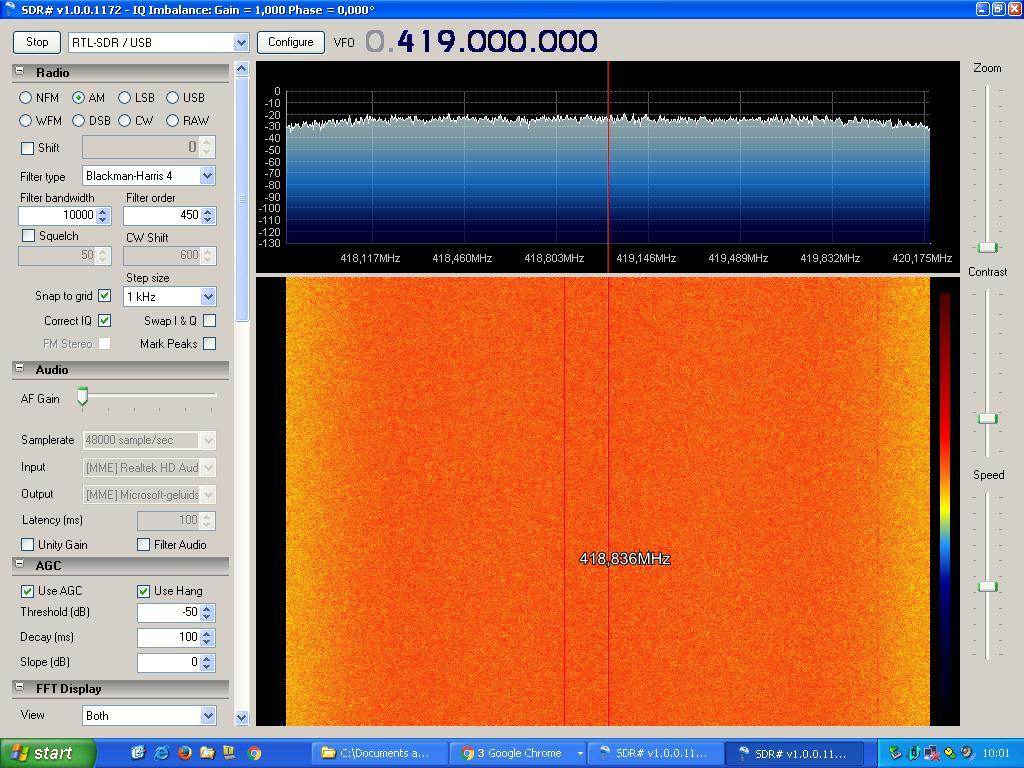
Op woensdag 13 januari heb ik geprobeerd met de Dwingeloo Radiotelescoop het signaal van een aantal pulsars op te vangen met een RTL-dongle. Als eerste heeft Paul Boven de schotel op pulsar PSR B0329+54 in het sterrenbeeld Giraffe gericht. Daarna heb ik het programma SDR# van SHARP gestart om een RFI stille band te vinden, bijvoorbeeld op 419 MHz (figuur 1).

Figuur 1 – SDR# van SHARP

Vervolgens heb ik SDR# afgesloten en het rtl_sdr.exe programma van Osmocom geopend. Na het starten van de meting met de juiste commando’s worden de data direct naar de harde schijf van mijn laptop geschreven. Mijn doel was een aantal opnames te maken en die thuis te analyseren om te zien of de pulsar te detecteren is met de dongle en hoe smal de bandbreedte kan zijn om nog succes te hebben. Hiervoor is de bandbreedte van de meting (in Herz = identiek aan de samplingfrequentie in Samples/second) ingesteld op oplopend 100 kHz (100 kS/s), 200 kHz, 500 kHz, 1 MHz en 2 MHz. Elke meting duurde 2 minuten.

Naast PSR B0329+54 stonden ook de pulsars PSR B0531+21 (de pulsar in de Krabnevel), PSR B2154+40 en PSR B2217+47 op mijn waarneemlijst. Deze pulsars zijn opeenvolgend zwakker, hebben een bredere puls of hebben meer dispersie.

Maar na de eerste serie metingen van PSR B0329+54 hoorden we een vreemd geluid vanuit de machinekamer: er bleek dat een verzonken bout op de kopse kant van de as waar de slinger voor de handbediening zit zich had losgedraaid. Hierdoor hebben we de waarneemsessie moeten beëindigen.

De 2 MHz (2 MS/s) meting

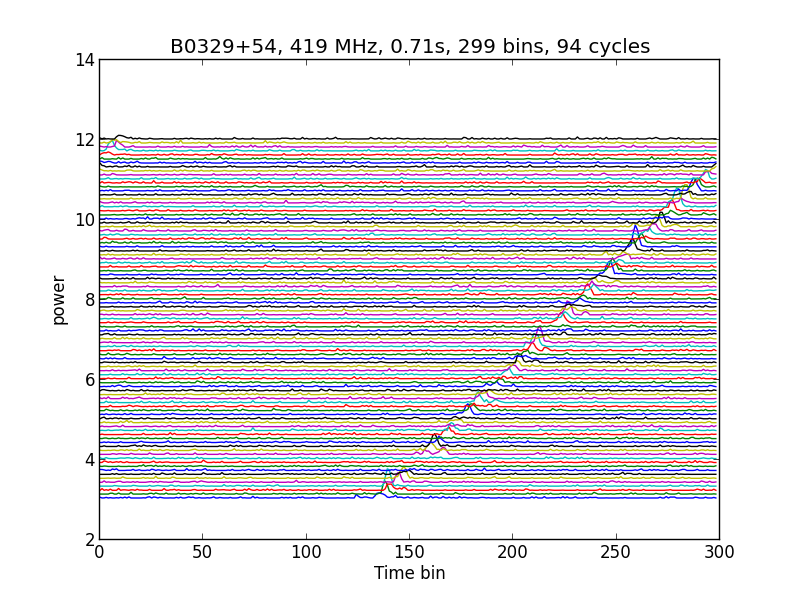
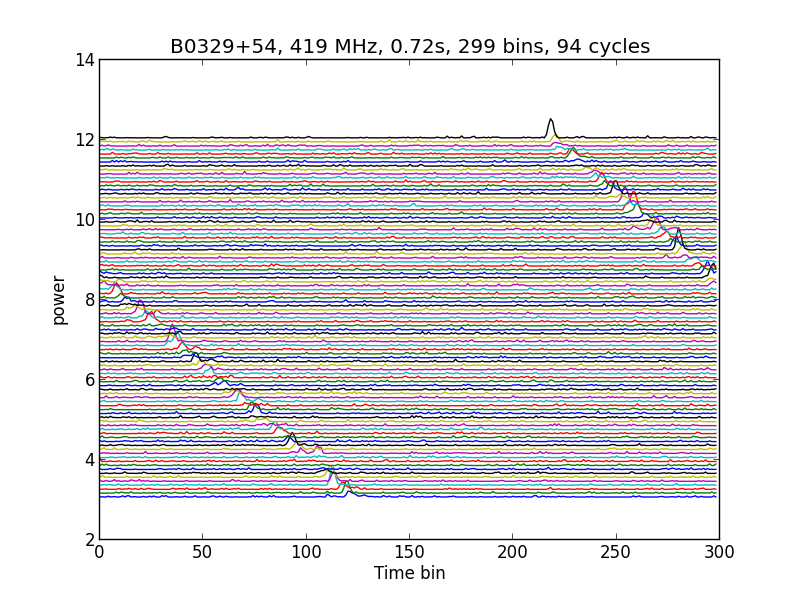
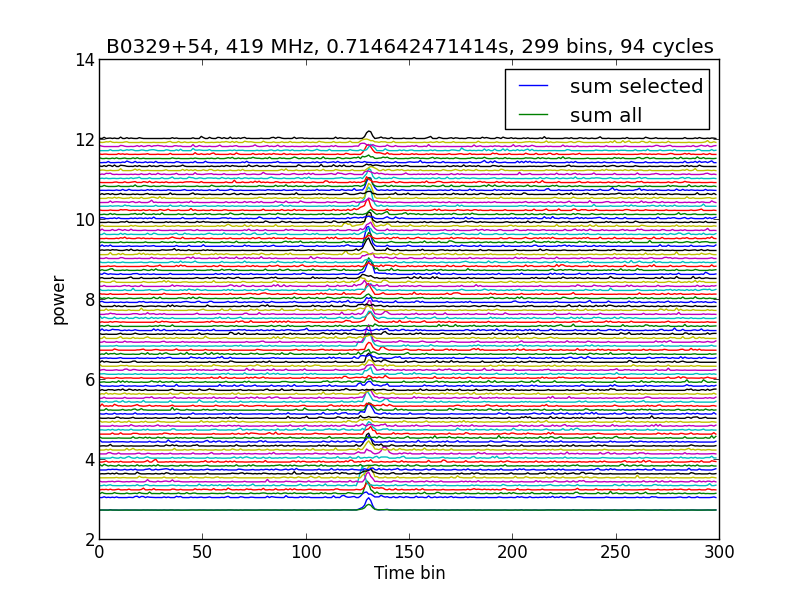
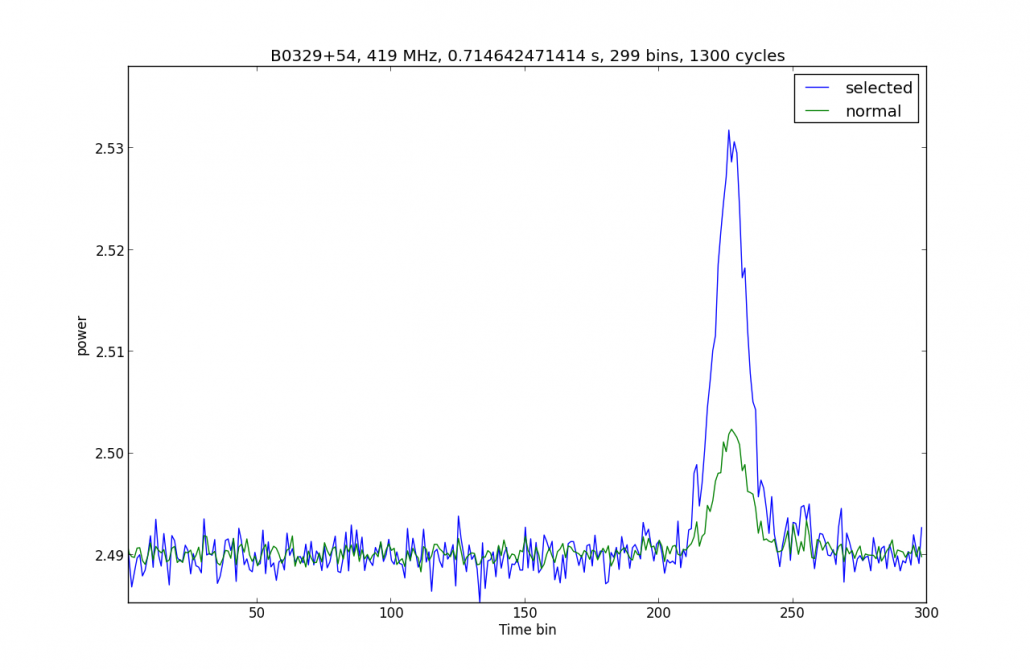
Na analyse thuis bleek dat de weggeschreven data goed was en kon ik de volgende plaatjes maken met mijn eigen Python analyseprogramma dat het signaal opknipt in stukjes van een periode zodat je alle periodes bij elkaar op kan tellen. Als je de pulsperiode ongeveer weet, bijvoorbeeld 0,71 seconde (figuur 2a), dan krijg je een bepaald resultaat. Een ander resultaat krijg je met 0,72 seconde (figuur 2b). Het beste resultaat krijg je met vouwen met 0.714642471414 seconde (figuur 2c).

Figuur 2a – 0,71 seconde

Figuur 2b – 0,72 seconde

Figuur 2c – 0,714642471414 seconde

Figuur 2d

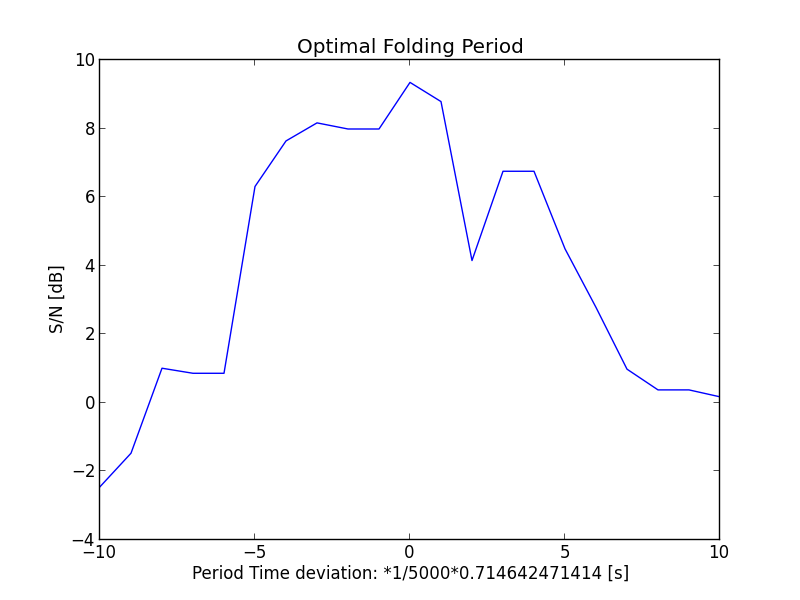
Je kan dit zelf berekenen/benaderen door een programma te maken dat de beste signaal ruis verhouding berekent en in een grafiek uitzet (figuur 2d). Je kan ook het programma TEMPO gebruiken dat mede is geschreven door Joe Taylor (Nobelprijswinnaar, astronoom en radioamateur) die de Dwingeloo Radiotelescoop na de restauratie in 2014 heropende.

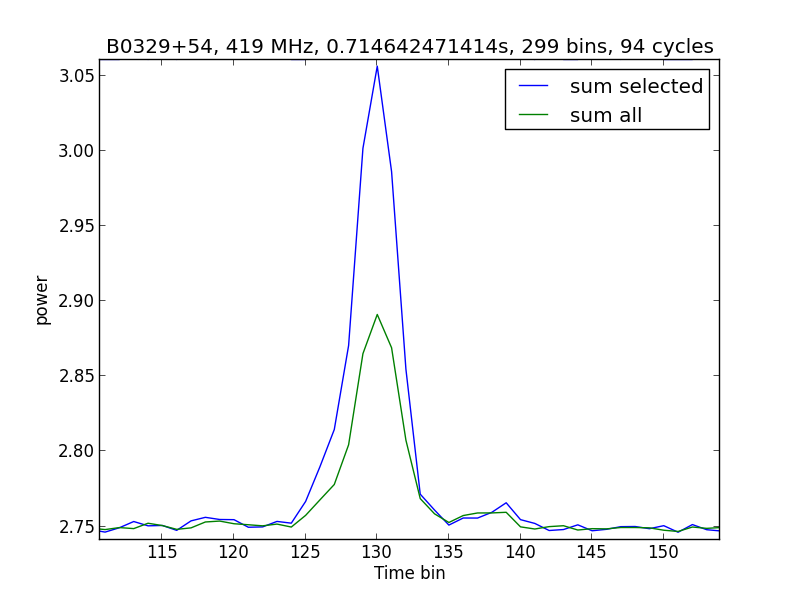
In figuur 2c staan de pulsen boven elkaar en kunnen ze opgeteld worden. Het resultaat staat in figuur 3a. De groene grafiek is gemaakt door alle lijnen bij elkaar op te tellen en de blauwe is gemaakt door alleen de lijnen met een puls bij elkaar op te tellen. Je kunt inderdaad in figuur 2c zien dat er een aantal periodes zijn die geen puls of een kleine puls bevatten. Dit komt door het scintillatie-effect, een effect dat lijkt het twinkelen van sterren. Dit radio-twinkelen ontstaat niet in de aardse atmosfeer maar wordt veroorzaakt door beweging van vrije elektronen in de interstellaire ruimte.

Figuur 3a – bandbreedte meting 2 MHz

Figuur 3b – bandbreedte 2 MHz gesplitst in 10 banden van 200 kHz

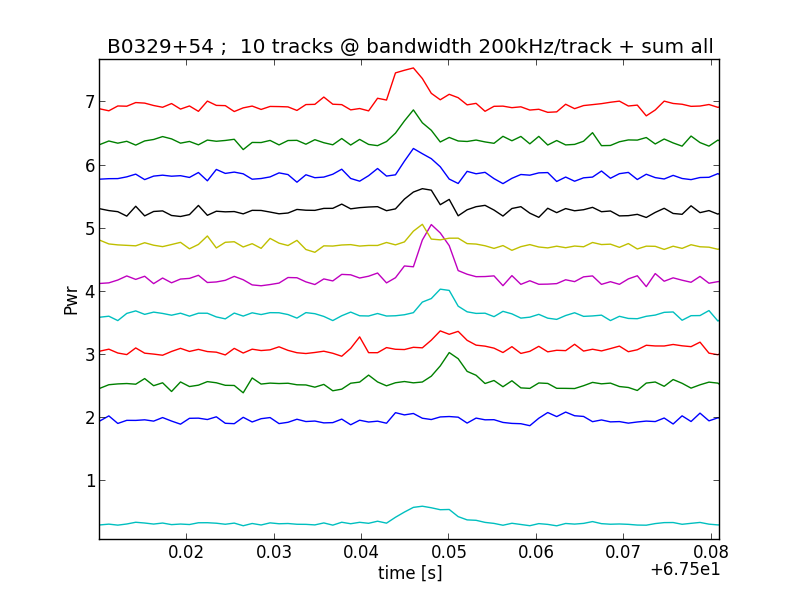
Het uiteindelijke plaatje lijkt nu compleet, maar dat is het nog niet. De grafiek blijkt nog steeds te breed. Dat komt doordat we bij de meting in een band van 2 MHz alle signalen bij elkaar opgeteld hebben. Als we de bandbreedte van de meting van 2 MHz opdelen in banden van elk 200 kHz en die onder elkaar zetten, zien we dat de pulsen niet op hetzelfde moment aankomen (figuur 3b). Een enkele puls bij 2 MHz bandbreedte was al zwak en door het opdelen in banden van 200 kHz wordt de puls nog zwakker, maar duidelijk is te zien dat de puls verschoven is in tijd. De hogere frequenties komen eerder aan dan de lage frequenties. Dit wordt dispersie genoemd; en dit wordt veroorzaakt door de vrije elektronen in de inter stellaire ruimte. Hoe meer elektronen er tussen pulsar en aarde zijn hoe meer vertraging. In dit geval blijkt de vertraging tussen het bovenste rode kanaal (419,9 MHz) in figuur 3b en het groene kanaal (418,3 MHz) 4,4 milliseconde te zijn. Op het onderste blauwe kanaal is geen puls zichtbaar. De lichtblauwe lijn onderaan in figuur 3b is de som van de 10 banden.

In de astronomie wordt de dispersie uitgedrukt in de dispersiemaat DM. In formule:

K = een constante
Δt = gemeten vertraging
f2 = laagste en f1 = hoogste frequentie waartussen de vertraging is gemeten

Voor deze meting komen we op DM = 24,4. In de literatuur vinden we 26,6 dus dit is een mooi resultaat voor een meting met een dongle.

Ik ben nog bezig om mijn programma dat de vorm van de puls berekent en tekent aan te passen zodat er voor de dispersie en de vertraging wordt gecorrigeerd.

Uit de pulsar periode kunnen we ook de diameter van de neutronenster berekenen en uit de dispersiemaat de afstand.

Het signaal bij een bandbreedte van 2 MHz lijkt zo goed dat je het wellicht ook direct met SDR# kan horen; ik heb dat nog niet geprobeerd.

De 100 kHz (100 kS/s) meting

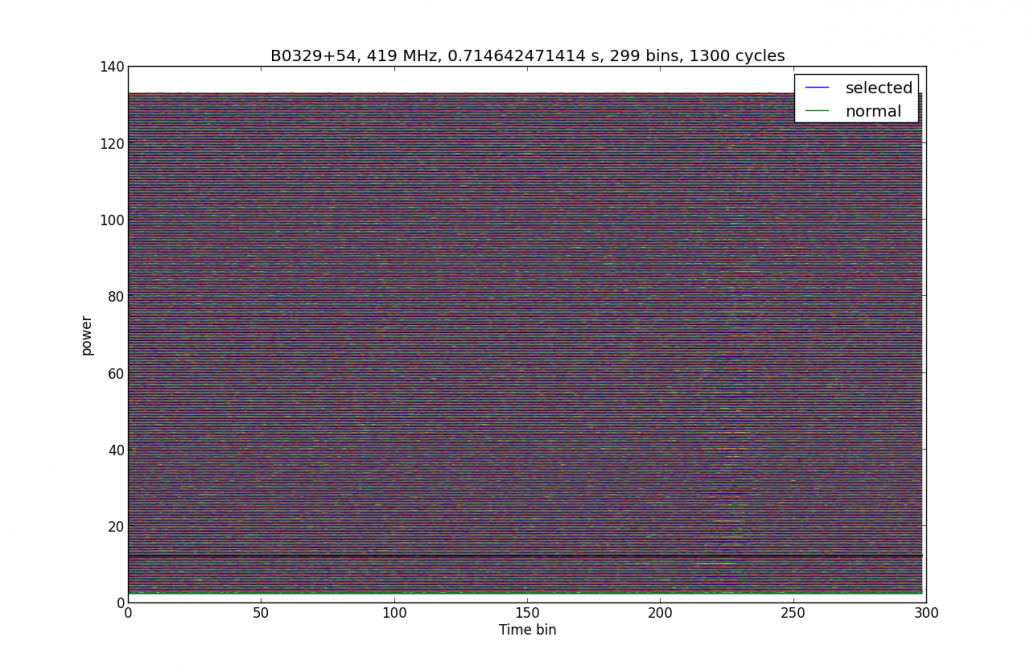
Het blijkt moeilijk om bij 100 kS/s ofwel 100 kHz de pulsar nog te zien in de ruis (figuur 4a, kijk goed rechts van het midden) maar wellicht is mijn analyseprogramma niet goed genoeg. Als anderen een beter alternatief hebben dan hoor ik dat graag. Ik ben nog bezig om de individuele pulsen zo uit te lijnen dat ze netjes kunnen worden opgeteld en zo een beter resultaat geven. Dat blijkt lastig.

Figuur 4a

Figuur 4b

Je kan wel weer mooi zien dat niet elke puls aankomt, sommige lijnen vertonen geen puls. Als je toch alle pulsen zonder meer zou optellen dan werken die platte lijnen niet effectief mee aan de reconstructie.

Hier is de blauwe grafiek het resultaat van de optelling van alle lijnen en de groene grafiek de optelling van alleen lijnen die een puls bevatten. Ook hier zie je weer de pre- en de post burst om de hoofd puls heen. Er zijn diverse theorieën over, bijvoorbeeld een ring in ring kegel vanaf de pulsar. Zoek zelf maar eens op het web naar de laatste stand van zaken en de overeenstemmingen daarover in de wetenschappelijke literatuur.

De RTL-dongle

Figuur 5 – RTL-dongle met koelblok

Dit is de dongle, aan de soldeerzijde vlak geschuurd naar een idee van CAMRAS-er Hans Smit en geklemd op een omgekeerd koelblok uit een PC. Zo wordt de temperatuur drift (in gain en frequentie) zo veel mogelijk vermeden. Voor RFI vermindering heb ik nog een ferrietblok om de USB kabel geklikt.

Zelf meten en/of zelf rekenen

1. Lees ook dit bericht groups.google.com/forum/#!topic/camras-forum/FSm7sBnChn4 op het CAMRAS-forum met de precieze gegevens wat te downloaden.
2. Zelf meten gaat eenvoudiger door te werken met een commando. Daarvoor kan je een .bat file gebruiken bijvoorbeeld rtl_sdr -s 2e6 -f 419.0e6 -n 2e8 dump2000a.bin. De naam van de file is het commando, deze betekent: een samplingfrequentie van 2 MB/s op 419MHz, totaal 2M samples en noem de data file dump2000a.bin. Deze file is hier te downloaden www.parac.eu/downloads.htm.
3. Als je het eerdergenoemde programma TEMPO wilt gebruiken kan je dat downloaden bij www.k5so.com/Pulsars_2015.htm (maar zie tijdelijke opmerking bij downloadpagina van K5SO).
4. Wie zelf wil rekenen aan mijn metingen: de pulsardata staat in I & Q formaat op mijn website www.parac.eu/downloads.htm.
5. Gratis SDR# en drivers zijn hier te downloaden www.rtlsdr.org/softwarewindows.

Wordt hopelijk vervolgd, Michiel Klaassen.